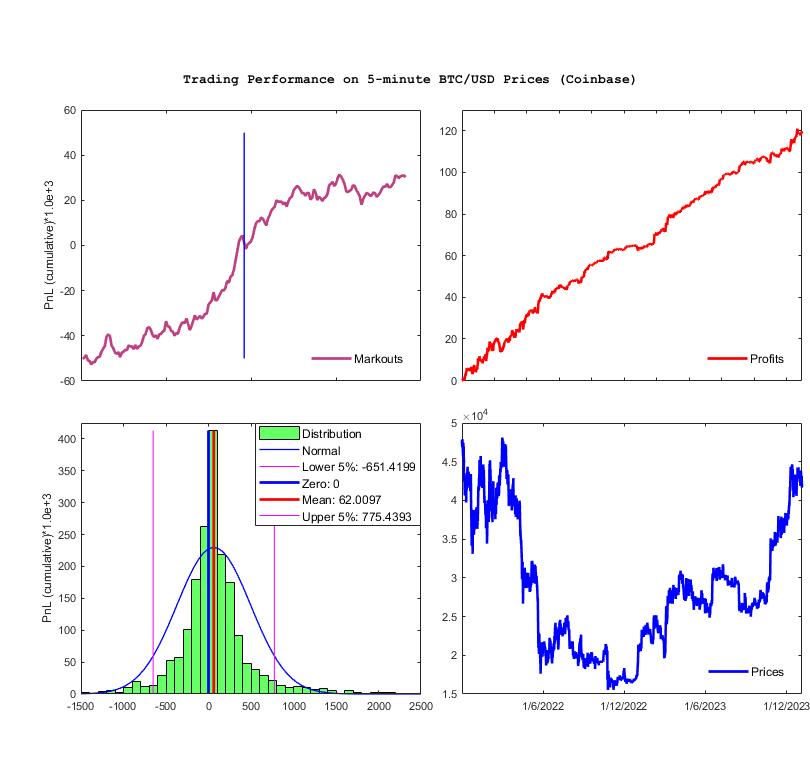
Cryptocurrency Trading using Asymmetric Local Learning. Asymmetric Local Learning is a new AI technology for modelling financial time series developed to facilitate building sucessful automated trading robots. The asymmetric learning helps to generate improved forecasts by efficient handling of the model over-prediction and under-prediction. This is achieved using asymmetric loss functions which penalize differently positive and negative fitting errors. Such cost functions help to capture more accurately the direction changes in serial data without emphasising the magnitudes of their deviations. Overall this flexibility enhances the ability to deal with heteroscedastic data contaminated by non-Gaussian noise when considered for local time series prediction. Furthermore, when considered for making trading systems it enables to tune the algorithm eventually to desired business objectives.
Our research developed a tool for automated cryptocurrency trading using asymmetric local learning. The training process uses a custom made loss function that treats differently the errors, and yields more accurate predictions which nake possible taking better pricing decisions. The efficiency of this trading machine has been tested rigorously by conducting a large number of simulations during which it showed a stable and highly profitable performance. Backtesting was carried out with BTC/USD prices downloaded from Coinbase and sampled every 5 minutes from 1/1/2022 to 21/12/2023. The statistics given in the plots are obtained using one-step-ahead forecasts to compute buy/sell signals for 1 Bitcoin (after paying fees of 1.5 Bps per trade and taking into account slippage). The numerical results are outstanding: ProfitPerTrade($) = 62.01, TotalReturn(%) = 402.85, MaxDD(%) = -14.63%, and SharpeRatio = 5.47.
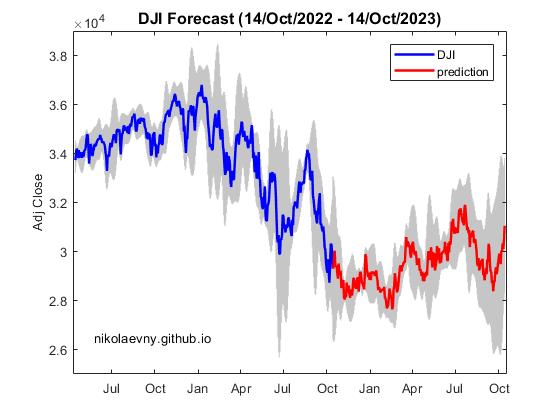
Effective Forecasting via Stochastic Machine Learning. Stochastic machine learning is a novel approach to computing predictions with high fidelity. It generates plausible forecasts of the expected erratic movements and trend changes in complex (irregular) financial time series. This is achieved with a nonparametric technology which includes sampling of subseries at different frequency intervals and quantization of the data at several levels (this helps to decrease the influence of the inhomogeneous noise in financial data). Theoretically speaking the quantisation levels are assumed to be states in a Markov chain, and the task is to estimate the transition probabilities in the Markov chain with which to generate predictions. The algorithm uses a memory of past segments (for each quantisation level) from which it selects patterns from the past with similar shape to the recent query segment and uses their continuations as the next states to build the most likely prediction. This helps to learn well the stochastic dynamics of the non-stationary data contaminated by large amounts of noise, like series of returns on prices.
Our research designed a forecasting algorithm based on the principles of stochastic local learning especially for making financial predictions. The particular implementation of the algorithm removes the linear trend in the prices in advance, and then performs extrapolation of the remaining data (after converting the prices into series of returns). The Markov chain has been made using 6 states. Local learning has been performed using the Euclidean distance as similarity measure to search for patterns in the history of each level with embedding dimension 15. The plot illustrates the multi-step ahead daily predictions for one year ahead of the Dow Jones Industrial (^DJI) index generated by stochastic machine learning.
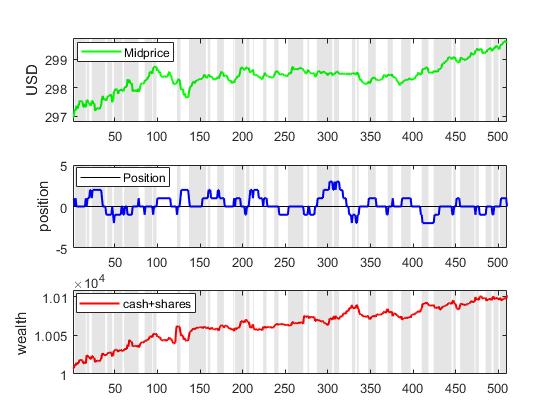
Market Making via Bayesian Learning with Nearest Neighbors. Automated market making (MM) is accomplished with algorithms that place simultaneously buy and sell orders for a given asset, seeking profits from their price difference. This kind of high-frequency trading algorithms [6] constantly readjust the orders to buy at lower (bid) prices and sell at higher (ask) prices so as to maintain and earn their difference (called spread). The task is to set such prices that get enough executions for achieving maximum profits with minimal risk. Setting the bid and ask quotes requires computation of the future spread or alternatively discovery of the future mid-price (average of the best bid and ask prices). The MM mechanisms include also procedures for inventory management that are necessary to control the exposure risk arising from large price movements.
Our research developed a market making algorithm using Bayesian learning to infer the expected mid-price as suggested by information-based models, and the mid-price is next plugged in an inventory-based model to calculate the bid and ask quotes. The originality in our approach is that the information about the fundamental value of the stock is collected using nearest neighbour search, and then used to update in online manner the probability density of the mid-price. This algorithm performs local density approximation in the vicinity of the closest temporal patterns chosen with an appropriate distance measure. The rationale is that similar deterministic trends may persist for short periods during the evolution of the price. The k-Nearest Neighbour (kNN) method is applied to find close patterns (neighbors) of the recent trend ending at the last point, and such nearest segments are exploited to make probabilistic predictions for the mid-price. We designed an adaptive Bayesian Nearest Neighbor Tool for extrapolation of mid-prices using a normalized kernel as weighting function. The kernel bandwidth is kept fixed to maintain a stable balance between the bias and variance.
Local Prediction of Mid-Prices in Limit Order Book Markets. The modern financial exchanges operate using Limit Order Books (LOB). The order book handles the buy/sell orders of an asset, depending on their price, size (quantity) and arrival time. The orders on the electronic markets are sent by algorithmic trading machines that execute sophisticated strategies at high-frequencies. A trading algorithm can be successful if it predicts the movements of the asset prices/returns, otherwise simply relying on historical data is not sufficient for taking profitable trading decisions. The machine learning research offers efficient approaches that can be used to predict the movements in series of financial prices/returns, like local learning using the k-Nearest Neighbor (kNN) algorithm. The kNN is a proper algorithm for nonparametric modelling of temporal data with complex dynamics. It builds the prediction using local dependencies, without training a global function model.
Our research developed a Local Trading Machine (LTM) for prediction and exploitation of the mid-price dynamics in limit order books. The LTM is based on the kNN regression algorithm, elaborated to manipulate high-frequency financial time series of returns on prices. The main distinguishing aspects of our computational tool are: 1) it seeks similar temporal patterns in the past with an adaptive distance metric for elastic matching through invariant transformations of the patterns (this helps to achieve more faithfull comparisons between segments of erratic data); and 2) it performs integrated forecasting using LOB imbalances (this helps to tune the outputs with respect to the supply and demand in the order book). These techniques make the operation of the kNN more resilient to the inherent noise and non-stationarity in series of returns. Since the algorithm flexibly reconstructs the series dynamics, it is able to react quickly to changes in the data and this facilitates composition of more accurate short-term forecasts.
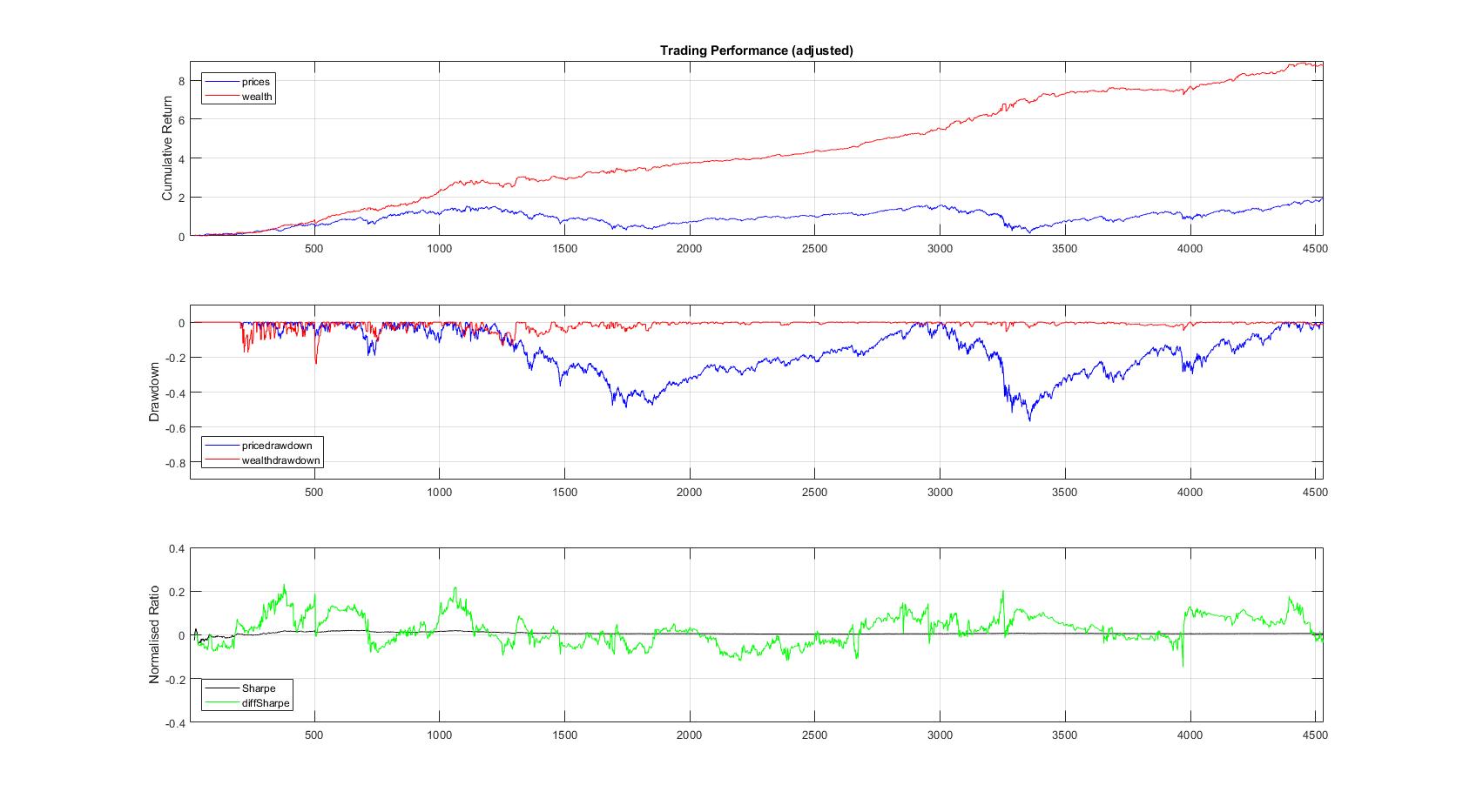
Automated Algorithmic Trading using Recurrent Reinforcement Learning. Automated algorithmic trading systems become increasingly popular due to the electronic nature of the transactions executed on many of the current stock exchanges. Making such quantitative trading systems involves the elaboration of optimal intelligent trading agents that bid on the market (rather than on discovery of equilibrium prices). The design objective is to construct profitable trading agents, not only to simulate the market evolution. The trading agents are expected to learn continuously to trade on the market, assuming that it is populated by other agents with pre-programmed behaviour and also market makers.
Our research developed an intelligent trading agent whose behaviour is controlled by a dynamic recurrent neural network using reinforcement learning. This agent is trained using recent market information to improve its bidding strategy and to become more efficient. The network is given as inputs returns from midprices (in the middle of the bid/ask spread) and predicts the midprice change direction, which helps us to generate useful trading signals. The agent learns to maximize the Sharpe ratio criterion, instead of learning to predict prices (or returns). The neural network training algorithm reinforces the agent performance using feedback action signals without forecasting returns and without explicitly provided targets from an external supervisor. Thus, the learning agent is stimulated to achieve higher profits with lower risk exposure, that is to take decisions leading to reduced risk performance via rewards with the Sharpe ratio.
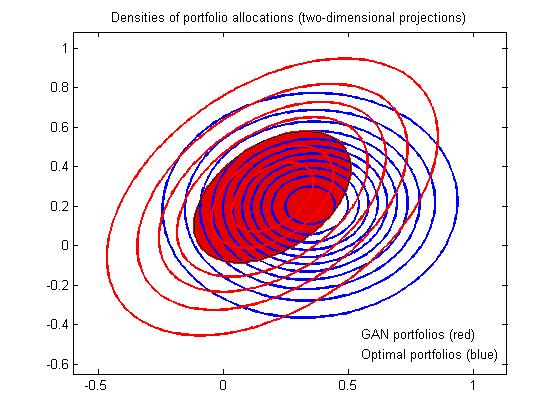
Generative Adversarial Networks for Machine Learning of Constrained Portfolios. The mean-variance portfolio (MVP) theory is a fundamental framework for rational investment management. It provides formulations for building profitable portfolios with reduced risk, which are extended by adding various constraints (like budgeting, no-shorting, leveraging, etc.) to ensure their practical usefulness. The constrained formulations often lead however to non-convex optimization problems that are difficult to solve even by the well known Quadratic Programming (QP) approach.
Our research developed a machine learning tool for constraint portfolio optimization using a Generative Adversarial Network (GAN). The GAN is a composite model of a generator network and a discriminator network that play adversarial game in which each tries to influence the other, while being controlled by different parameters. The generator learns to produce samples from the distribution of the data. The discriminator evaluates the feasibility of the drawn samples and decides whether they are realistic or fake. We designed the generator using a Deep Neural Network (DNN) for representing synthetic distributions of portfolio weights (stock allocations). A uniform random prior is passed as input, propagated forward through the network, and the network output returns a weights vector sample (without forecasting returns on prices as in some previous works). The discriminator applies analytical formulae to compute optimal weights which suggest a reference mean-variance portfolio for comparisons. During the optimization process the discrepancy between the assumed optimal weights and the sampled weights decreases, and the generator converges to a better estimator of the weights distribution leading to portfolios with improved performance. The advantage of this approach is that it has capacity to learn fast the weights distribution in nonparametric fashion.
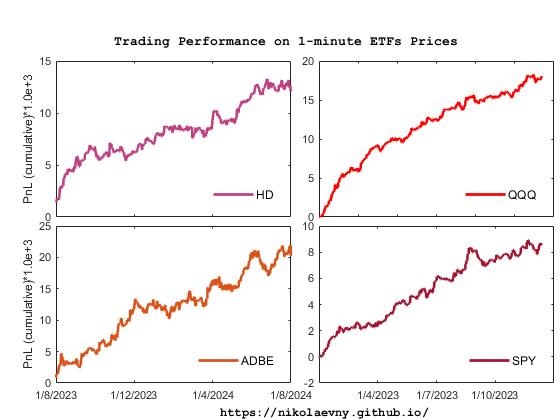
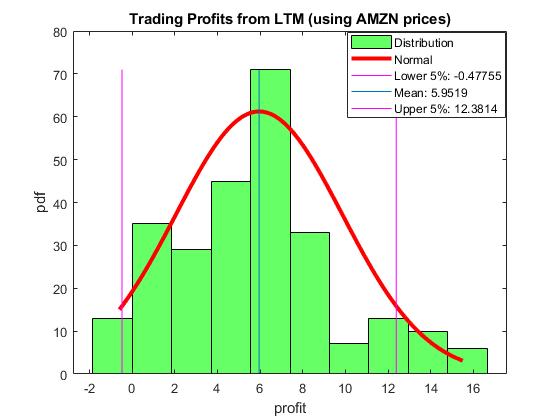
Local Quantile Prediction for Trading Machines. Local prediction algorithms are especially suitable for financial time series which usually exhibit dynamic statistical characteristics and non-homogeneous noise. Their learning potential can be extended further with quantile prediction to adapt even more flexibly to the changes in the distributions occuring in different time periods. The rationale is that quantile modelling infers ranges of potential future values, that is it infers interval forecasts efficiently without overfitting the given training data. Such local quantile prediction can achieve better generalisation when applied to financial data with large amounts of noise (because it provides ability to capture well the behaviour of skewed serial data contaminated also by outliers without assuming a specific parametric distribution for the dependant variable).
Our research developed a Local Quantile Prediction (LQP) algorithm ttat learns adaptively from financial time series of returns on prices. Extensive walk-forward analysis showed empirically that the LQP helps to build intraday trading machines with robust economic performance. The figure below illustrates the accumulated profits on several 1-minute ETFs price data from one year each. The particular conditional quantiles for each asset are selected thourgh experimentation. The results (accumulated PnL) are computed using one-step-ahead forecasts to generate buy/sell signals for 100 shares and take into account commissions of 0.002 per share. The simulated trading sessions started at 9:30 and terminated at 16:00.
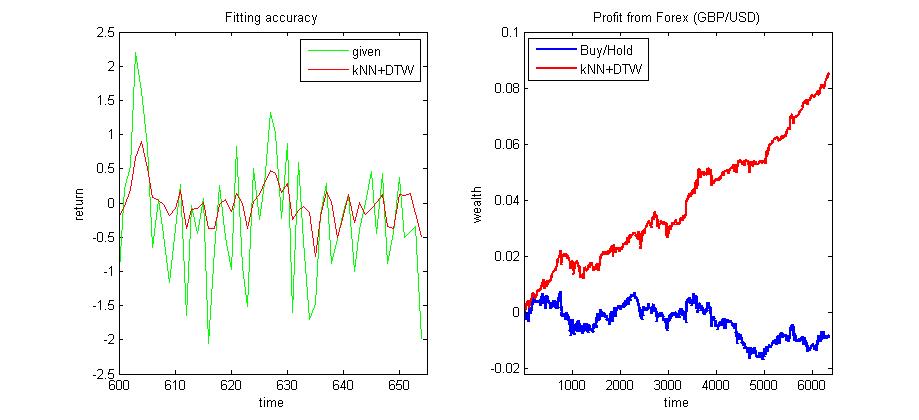
Machine Learning with Dynamic Time Patterns for Algorithmic Trading. The algorithmic trading frameworks typically include estimation of time series models often performed through machine learning. Handling financial series of prices/returns is a very difficult task, however, because they are randon fluctuations (more precisely they are commonly assumed to follow standard Brownian motion). That is why, the popular global function models can not capture global mappings in such series and can not forecast well. Applied to financial time series of prices/returns the global function models simply produce outputs with time delay (phase lagging) that are useless for algorithmic trading. When addressing such tasks one should rather look for solutions with alternative local models, like the k-Nearest Neighbors (kNN) algorithm. The kNN provides a technique for computing the probability density function of the data using only selected close patterns (neighbors) to the query.
Our research developed a nearest neighbour based machine learning tool (kNN-DTW) for nonparametric forecasting of time series using dynamic time patterns. The tool has two distinguishing features: 1) it implements an original statistical DTW for robust matching of temporal patterns, which uses standardization of the distance norm by the volatility of the series (this prevents the comparisons from distortions by abnormal noise, and helps to obtain results with close volatility to the current situation); and 2) it implements individual weighting of the neighbors. These features together make the kNN-DTW tool more noise tolerant, and more accurate on predicting real-world financial time series. The experimental results on intraday exchange rates series indicate that the novel kNN-DTW machine outperforms the other nearest neighbour based algorithms, using alternative contemporary distance measures, as it achieves higher profits with lower risk.
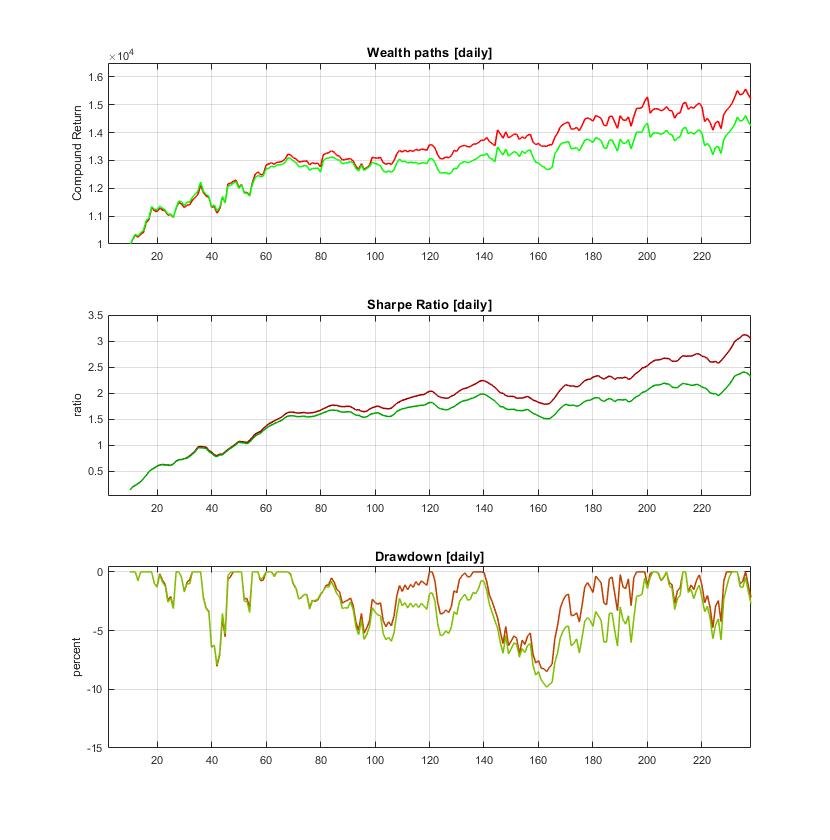
Efficient Direct Reinforcement Learning of Low-risk Portfolios. Reinforcement Learning (RL) shows encouraging results for computing automated investment strategies. The RL paradigm offers procedures that easily accomodate risk-adjusted performance functions and facilitate portfolio optimization without forecasting models. The RL algorithms continuosly maximize the objective function by taking actions without explicitly provided targets, that is using only inputs and feedbacks on their performance. This algorithmic capacity to take behavioural decisions makes them especially convenient for the design of reliable portfolio trading systems. The two main RL methods currently studied as alternatives for financial portfolio construction and trading are: 1) value-based (Q-learning), and 2) policy-based (Direct Reinforcement) learning. ). The theoretical and empirical studies recommend the Direct Reinforcement (DR) learning as a potentially better mechanism for finding profitable portfolios.
Our research developed a Connectionist Reinforcement Learning machine for efficient computation of Online Portfolios (CRLOP). This is a multi-output feedforward neural network where each network output generates allocation for a particular asset in the portfolio and the inputs pass lagged returns from the corresponding asset prices. The network is trained with an original hybrid risk-return optimization function, which includes the Sharpe ratio and an additional term that accounts for the risk asymmetrically (this term discounts the effects from the loosing trades). This is necessary to overcome the equal treatment of high profits and heavy losses in the symmetric standard deviation formula. During training the network adapts the weights to achieve higher portfolio profits with low-risk by sensing the returns and using them to reinforce its performance without fitting the data. The allocations are obtained incrementally in forward manner by passing the data through the network and modifying the weights (with immediate rewards from the previous results) using a modern stochastic training technique.
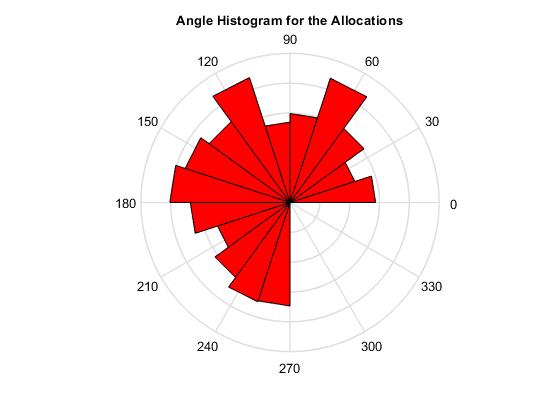
Deep Neural Networks for Prediction-based Portfolio Construction. Connectionist learning offers powerful modern technologies for quantitative modelling that can be used to reduce investment risk. It provides highly nonlinear models which are convenient for describing multivariate time series of returns on prices. Such connectionist machines that become increasingly popular in financial engineering are the Deep Neural Networks (DNN). The DNN have already been applied to predict stock returns for building portfolios. The most popular deep networks for such tasks include the recurrent Long-Short Term Memory (LSTM) neural networks, the Deep Multilayer Perceptrons (DMLP), and the Convolutional Neural Networks (CNN). The attractive fundamental concept underlying all these deep networks is nonlinearity. The nonlinearity is especially important when searching for models that generalise well, that is perform well on unseen future data.
Our research developed an original Robust DNN (RDNN) model with rectified and sigmoidal units especially for building prediction-based portfolios. This is a multi-output network that captures time relationships in the data using a short-term memory through a tapped delay line from lagged observations. The major technological innovation in the RDNN is that it overcomes possible disturbances from outliers using the heavy-tailed (Student-t) noise distribution. Adopting the Student-t distribution for the noise is important for handling practical financial time series because the estimates can be affected severely by atypical observations. Moreover, the departure from Gaussianity affects the model selection and may lead to choosing a model with wrong complexity. We obtained robust derivatives are plugged them into a contemporary stochastic gradient descent training algorithm. The RDNN attains good generalization as it avoids overfitting using two techniques: structural sparsity (attained with the rectified units which induce sparsity) and dropout (which helps to avoid overtraining with the provided examples).
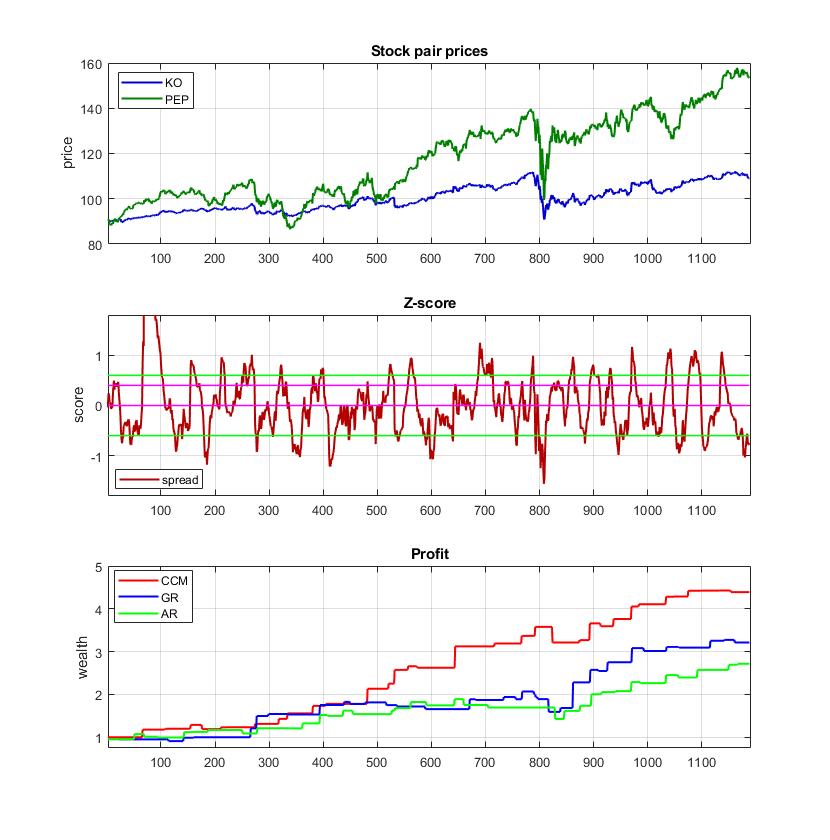
Universal Cointegration for Pairs Trading via Machine Learning. Pairs trading exploits arbitrage opportunities arising when the prices of two stocks with common trends diverge temporarily from their average relation. Statistical evidence for stable long-term common movements in price series can be obtained with the cointegration measure. The presense of cointegration facilitates the implementation of mean-reverting trading strategies. One modern approach is to search for universal cointegration using the method of Convergent Cross Mapping (CCM) which assumes that a pair of series feature the same dynamics, and seeks to reconstruct it by a common function of past temporal patterns (known as neighbors). The CCM uses the k-Nearest Neighbor (kNN) algorithm to look for nearest neighbors in each of the series that can be coupled in a cross-mapping.
Our research developed a pairs trading tool based on universal cointegration elaborated with the CCM method. The CCM reproduces the causal dynamics of pairs from time series by constructing a mutual function that takes close temporal neighbors as arguments. We designed a specialized kNN algorithm for local machine learning from interdependent financial time series. This kNN algorithm has two original, distinguishing aspects: 1) invariant nearest neighbour selection- it calculates similarity after making adjustments to the amplitudes and periods of the candidate patterns; and 2) mutual centroid prediction- it computes future time series values by combining data from coupled nearest neighbors and distance-based weighting the succeeding points after the precedents. This is a self-adaptive, noise-tolerant learning mechanism whose output is tested to determine whether universal cointegration between the given series exists. The significance of the series association is evaluated with the Pearson correlation coefficient.
Deep-Memory Networks vs. Deep Learning Networks for Stock Market Prediction. The Deep Learning Networks (DLN) are popular tools for machine learning. The power of DLNs is in their ability to discover complex functions of real-world noisy data by composing hierarchically simple representations, technically speaking they learn to generalize by extracting features. The good results of DLN on data mining tasks motivated researchers to seek improved results in financial forecasting as well. There have been reported applications to modelling: exchange rates, stock returns, market indices, etc. The problem is that the application of DLNs to stock market modelling is not straightforward, and their suitability for such tasks has not been yet fully investigated.
Our research invented a novel tool Deep-Memory Neural Networks (DMNN) for machine learning from financial time series and stock market forecasting. The rationale for making deep memory networks for stock market prediction is that financial time series often feature slowly decaying autocorrelations and this requires long-memory embeddings. The DMNN model takes lagged input vectors of predetermined depth, and is treated as a dynamical system using sequential Bayesian estimation to accommodate properly the temporal dimension. Thus, during training the DMNN becomes fitted to its full potential of being a dynamic machine that learns time-dependent functions, and this is its essential advantage over the other DLNs which are typically trained as static functions. There are implemented various filters that make the DMNN behave like nonlinear autoregressive models with time-varying parameters.
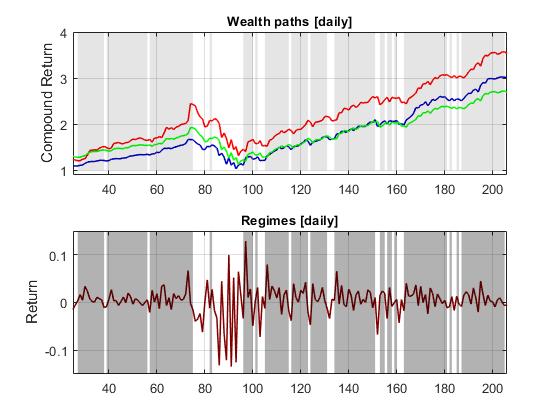
Regime-based Machine Learning of Green Stock Portfolios. There is widely accepted empirical evidence in finance that the patterns in the markets change over time, and the assumprion is that prices are not generated by a single economic regime. The prevailing opinion is that the stock markets evolve through bullish and bearish periods. This suggests that portfolio managers should vary the invested asset proportions with the shifts in market behaviour. The econometric research already designed regime-switching (RS) models, that account for assumed changes in the economic variables. These are sophisticated models which identify abrupt structural alterations in the dynamics of asset prices. There have been reported various applications of these RS models to portfolio construction tasks. The key idea is to achieve optimal asset allocations via extraction of regimes in the market fluctuations.
Our research developed a computational tool for building portfolios under regime-switching. The rationale is that the exploitation of market regimes helps us to find more accurate model parameters. We assume that the returns of a market tracking portfolio follow a two-regime-switching model (alternate between bull and bear periods). The overall regime-based model reproduces realistically the occasional breaks in the mean, and allows us to create really good portfolios. A distinguishing feature of our tool is that we have implemented a Markov Regime-Switching (MRS) model. Its regimes are separated by distinct means and volatilities, while the lagged input coefficients are common for both submodels. The switching parameters are calibrated with the Hamiltonís filter, and the Kimís smoother. The two sets of asset betas are estimated using a Bayesian machine learning technique and next processed in a dynamic mean-variance setting. At each moment in time the portfolio weights are calculated dependent on the particular regime, that is the portfolio is conditioned on the regimes.
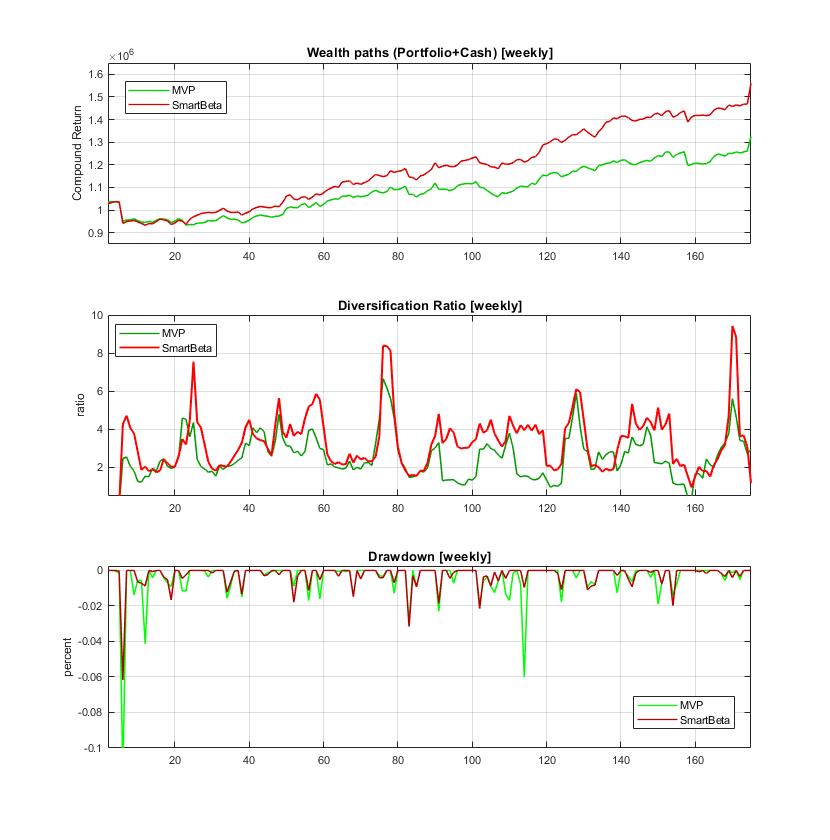
Building Smart Beta Portfolios with Large-Scale Machine Learning. Smart Beta portfolios offer the investor possibility to choose exposures (betas) to specific factors that are assumed to be driving the market evolution. This is a strategy that seeks smart asset allocations using risk control schemes, rather than using traditional capitalization weighting. The aim is to outperform the market with balanced risk reduction via increased diversification (using measures that depend on correlations and volatilities, but do not depend directly on expected returns). The greater diversification brings reduced volatility and enhanced performance compared to other strategies like simple index tracking. The Smart Beta is usually implemented with less frequent rebalancing and is often classified as passive investment.
Our research developed a tool for computing low volatility Smart Beta portfolios using large-scale machine learning. The distinguishing contributions of our machine learning framework are: 1) a novel ADMM algorithm for constrained identification of Most Diversified Portfolios (MDP); 2) stochastic gradient descent training algorithms with analytical derivatives for quadratic optimization and tracking error minimization; and 3) an algorithm for predictive estimation of covariance matrices according to the method of moments. The ADMM is a kind of machine learning algorithm which is especially suitable for large tasks as it splits them into subtasks that are better tackled separately. The tool is elaborated to learn allocations for long-only positions with desired target returns (tuned with appropriately chosen risk-aversion parameter). If necessary the sparsity can also be tuned dynamically with an available cardinality parameter.
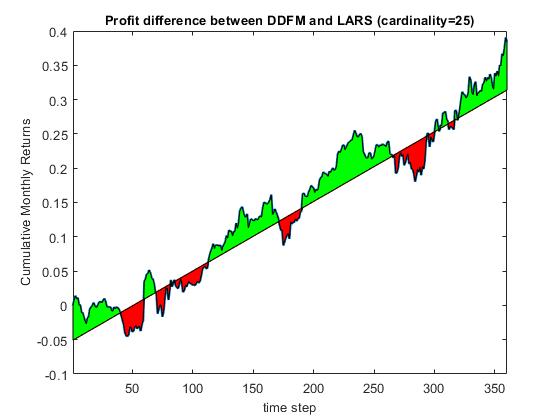
Deep Learning of Dynamic Factor Models for Asset Pricing. The large amount of transactions on the electronic exchanges today stimulates the development of computational algorithms for automated portfolio trading. These algorithms continuously optimize the portfolio with the arrival of new information on the market. The optimization strategy typically includes asset pricing, asset selection and rebalancing. A popular formalism for asset pricing are the factor models. A factor model describes the relationships between assets by regressing their returns on unobservable latent variables Such a model captures the dependencies between multiple return series into a small number of correlations. The difficulty is to choose only a subset of factors which taken together are profitable to trade, that is to select a parsimonious factor model.
Our research developed an original nonlinear dynamic factor model for asset pricing using a deep learning technology. We designed a dynamic factor model represented by a recurrent neural network with local memory that carries temporal information. The network is trained with a dynamic learning algorithm the BPTT (Backpropagation Through Time) which unfolds the model back in time to capture temporal dependencies. This is a deep learning mechanism because the unrolling creates a deep network structure. The BPTT is used to update the parameters of the hidden layer which produces the latent factors. The output layer computes the beta loadings. The strength of our model is that it predicts asset returns from inferred factor realizations, more precisely, the factors are forecasted arrangements of individual asset contributions to the overall portfolio. The overall model is a time-dependent function whose forecasts are less sensitive to noise and nonstationarities in the time series.
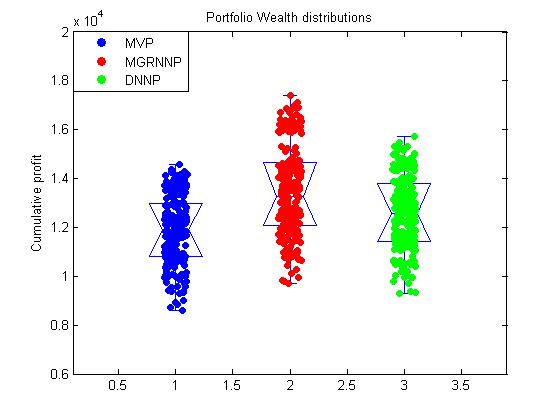
Overfitting Avoidance in Portfolio Construction using Probabilistic Neural Networks. Portfolio construction and many financial problem solving tasks involve modeling returns on prices. The popular approach is to take the means of the historic returns, but it does not lead to optimal portfolios. Efficient portfolios can only be built with predicted returns that peek into the future behaviour of prices. Since returns on prices are almost impossible to model and predict accurately, even plausible forecasts are acceptable in practice. The problem is that many researchers usually adopt standard function approximation models, which however are theoretically inconvenient. The reason is that returns are random fluctuations of a discrete Geometric Brownian Motion, and they can not be captured well by such function approximation models (like Neural Networks, Support Vector Machines, Gaussian Processes, etc.). Moreover, these models are trained with algorithms that seek to minimize the fitting error and this causes overfitting. That is why, these function approximation models models can not provide reliable predictions of returns.
Our research developed an original tool for portfolio construction based on the probabilistic GRNN model. The key idea is to represent the returns from the stocks in the portfolio with a multivariate distribution. The novel Multivariate General Regression Neural Network (MGRNN) forecasts simultaneously the returns of several stocks without assuming a specific functional form, and it learns a probability density. The MGRNN technology has three distinguishing features: 1) its network architecture has multiple outputs (there is a separate output for the mean return of each stock); 2) it has an individual spread parameter for each stock (thus the density shape is made proportional to the effective range of each particular stock), and these parameters are trained in a principled way using a second-order learning algorithm with analytical derivatives; and 3) it eliminates the unessential inputs by soft pruning (this reduces, sparsifies the model), and further helps to avoid overfitting. The advantage of MGRNN for financial time series prediction is that it generates local response to the testing input, instead of making global approximation which can actually cause distortions in modeling the current trend.
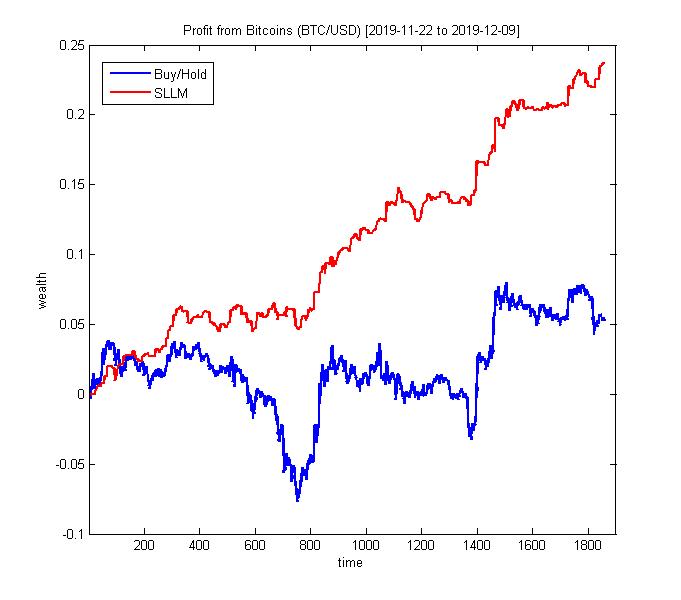
Nonparametric Machine Learning for Algorithmic Cryptocurrency Trading. The cryptocurrencies are attractive for algorithmic trading because of their high volatility on the stock markets. The volatility can be exploited by converting a sequence of crypto prices into an oscillating series and simulating mean-reversion trading: buy when the series moves higher than the equilibrium level, and sell when it reverses back. A trading algorithm takes such decisions after estimating the price movement direction through historical or predictive time series analysis. Trading is more profitable when the algorithm can look into the future evolution of prices. The problem is that it is extremely difficult and practically impossible to predict accurately the stochastic behaviour of prices/returns (they are assumed to follow a standard Brownian motion), so the task is to produce useful forecasts for their immediate trajectory. This can be accomplished with a proper description of their dynamics, and a corresponding learning mechanism like the nonparametric machine learning.
Our research developed a Self-adaptive Local Learning Machine (SLLM) for nonparametric prediction of financial series of returns on prices. The SLLM implements the nearest neighbor method with two distinguishing features: 1) it performs neighbours selection using an adaptive distance metric which evaluates closeness after linear transformation of the data patterns, that is the machine looks for similar shapes in the movement of returns by sliding the query across the historical returns while stretching, shrinking and amplifying the patterns; and 2) it performs distance-based extrapolation through local averaging proportional to the degree of similarity with the query vector, thus the forecast reflects the essential characteristics of the data trajectory. The SLLM is elaborated to generate forecasts of returns for algorithmic cryptocurrency trading. The return forecasts are converted to prices, and next taken to compute the residuals between the forecasted prices and the mean price from the most recent past. The crypto trading strategy parameters are obtained by treating the residuals as a mean-reverting (Ornstein-Uhlenbeck) process.
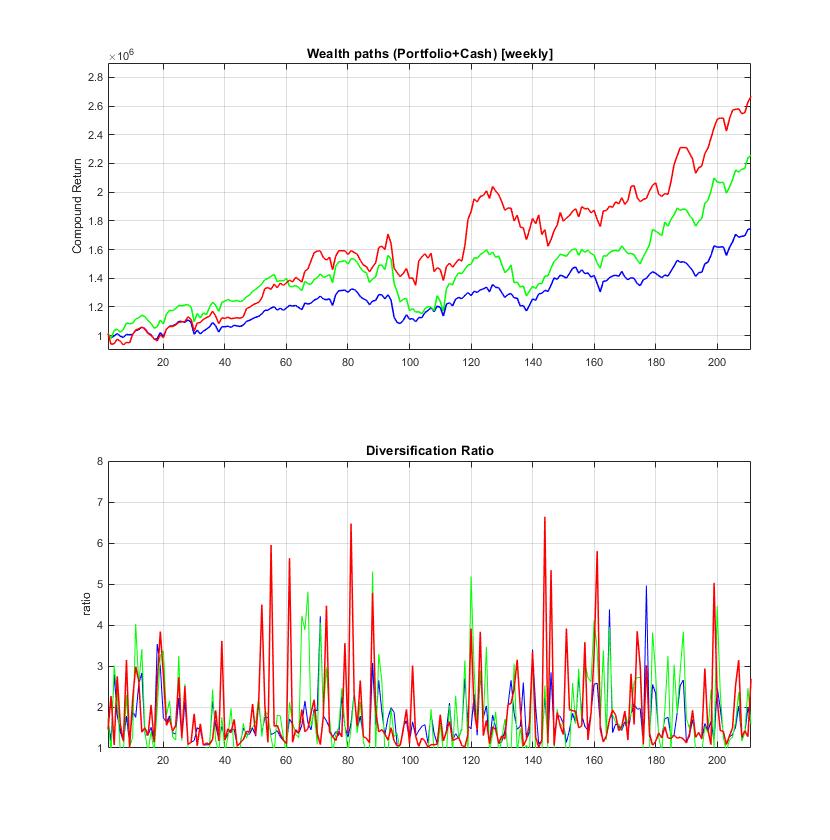
Efficient Computation of Sparse Risk-based Portfolios using Machine Learning. The risk-based approaches to portfolio construction are modern alternatives to the Markowitz approach to asset management. These approaches seek portfolio allocations that diversify the risk, rather than capital allocations. The rationale is that a proper diversification can enhance the profits as it can be more resistant to market fluctuations. This is achieved by balancing the exposure to higher-risk assets with lower-risk assets, so that less volatile assets receive increased weights. Such portfolios are computed with optimization routines using risk diversification measures. These measures are defined by functions that depend on the asset volatilities, and the total portfolio volatility but do not depend directly on the returns of the individual assets.
Our research developed an efficient (reliable and fast) tool for finding sparse risk-based portfolios using a machine learning algorithm. This is a universal tool which simultaneously perfroms portfolio selection and diversification while searching for asset allocations. Its distinguishing feature is a projection algorithm that jointly selects and estimates constrained weights efficiently with explicit update equations (without running procedures for quadratic programming). The learning algorithm minimizes iteratively the objective function in one direction at each time step, and also accomodates cardinality constraints to obtain sparse results. Technically speaking, the algorithm minimizes successively quadratic loss functions by computing Euclidean projections in a greedy manner. It is different from the primal projected gradient search algorithm which does not facilitate sparsity. That is why, the tool is especially suitable for solving high-dimensional risk-based portfolios with capital constraints.
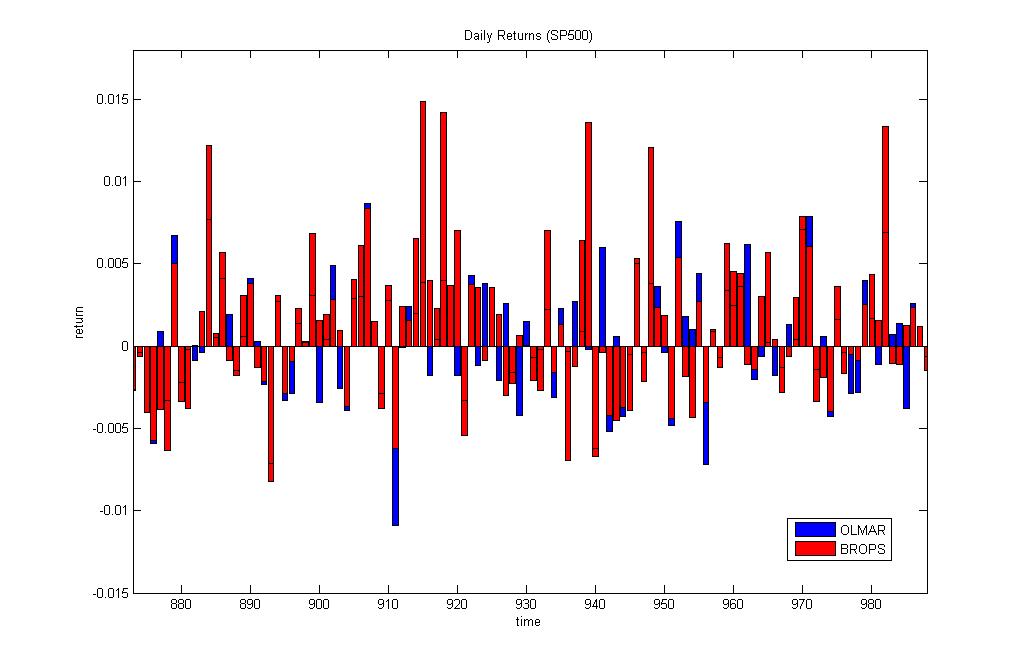
Bayesian Machine Learning for Robust On-line Portfolio Selection. The predominant amount of trades on the biggest stock markets in the world are currently done automatically. Electronic trading is conducted using various kinds of algorithms, like for example portfolio robo-advisors. Such on-line portfolio selection algorithms calculate asset allocations sequentially with the arrival of stock price data. At every time instant when stock prices arrive the allocations are re-estimated to take into account the new information from the market. The objective of on-line portfolio investing is maximization of the cumulative wealth with minimum risk. The allocations (weights) indicate the portions of wealth to be transferred between the assets. The activity of buying and selling corresponding fractions of assets is called rebalancing.
Our research developed a robust on-line portfolio construction tool using Bayesian machine learning. We apply variational Bayesian inference to derive a learning algorithm for robust regression, which is especially suitable for processing financial time series typically contaminated by large amounts of noise. The original feature of our tool is a Bayesian learning algorithm for calibrating heavy-tailed models of returns on prices (based on an approximation of the Student-t density by an infinite mixture of Gaussians). After pre-processing the price series with this algorithm, sequential estimation of the weights is accomplished with stochastic gradient descent search for solving the portfolio optimization problem. The optimization problem involves minimizing the deviation from the previous weights, and the distance from the mean reversion threshold. The motivation is to keep the portfolio close to the previous one, and to rebalance it when the return increases above the threshold. The threshold parameter is estimated at every time step using a discrete version of the Ornstein-Uhlenbeck stochastic differential equation.
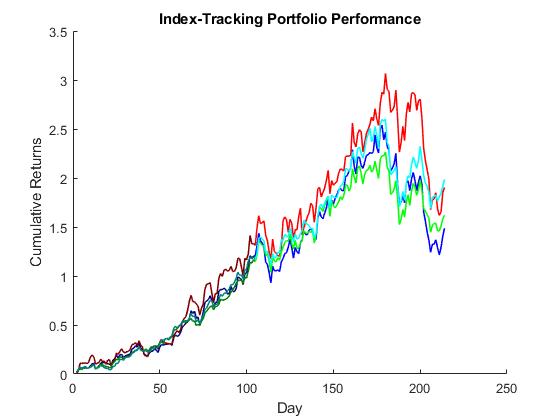
Deep Learning of Small Portfolios for Index Tracking with Reduced Risk. Index tracking is a popular investment strategy for building portfolios of assets that replicate closely the movement of a benchmark index. The key idea is to find optimal subsets of assets (partial replication) that regularly outperform the market. This is accomplished by extracting a few representative assets that can be traded with less transaction costs and reduced risk. The management risk can be reduced using small portfolios which faithfully represent the hidden structure of the market (that is, the relationships between the index constituents), and decrease the exposure to unimportant assets.
Our research developed an original approach to building small portfolios through deep learning of sparse autoencoder (SAE) models. The SAE models are trained using specialized topology reshaping techniques which help to identify less complex models that capture the essential structure in the data. We elaborate two techniques that enforce reshaping: 1) soft sparsification with size-adjusting regularization that drives the irrelevant hidden node outputs to zero, and 2) hard sparsification by explicit pruning of redundant hidden nodes without loss of accuracy (using predefined importance criteria). The desirable sparsity level (percentage of nodes to be truncated) is controlled with a cardinality parameter which allows to set the desirable size of the investment. The SAE are also made robust to error fluctuations using the heavy-tailed (Student-t) density to handle the output noise. This improves the learning dynamics in addition to using modern stochastic gradient training algorithms. The practical effect from such robust treatment of the model is lower variability of the results and risk reduction.
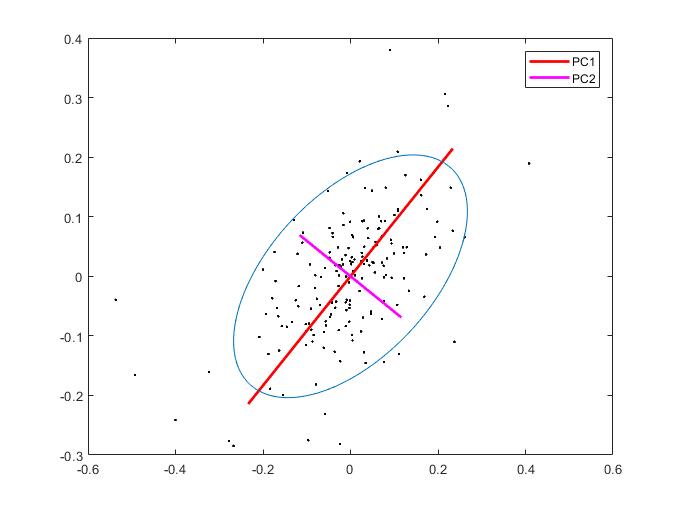
Deep Learning Autoencoders for Building Principal Component Portfolios. Portfolio arbitrage is a practical economic task that searches for profitable investment allocations in a selected universe of stocks. The dynamics of multiple financial price series from a portfolio of stocks may be considered to be driven by a number of common economic factors as well as idiosyncratic terms. This idea stimulates the research into machine learning methods which investigate hidden factor models of cross-covariances between asset prices. Two popular methods for finding latent factors are the Principal Component Analysis (PCA) and the Autoencoders (AE). They help to discover combinations of stocks (market factor) that explain most of the variance in the selection (systematic risk). Having such factors facilitate the creation of market neutral portfolios by treating the remaining idiosyncratic risk as a mean-reverting (Ornstein-Uhlenbeck) spread process.
Our research develops efficient portfolio trading tools using Autoencoder networks that discover principal components via Bayesian treatment of the model. Following Variational Bayesian inference we obtain analytical formulae for all model parameters (including the noise variance and the individual regularizers for each weight). The AE performs weighted encoding of the inputs into a lower dimensional space, and next weighted decoding of the compressed copy back to an approximate version in the original space (using a non-Gussian reconstruction error model). The inferred weights, corresponding to the eigenvectors of the covariance matrix, are taken to calculate the allocations for the stocks in the eigenportfolio. More precisely, we construct an eigenportfolio as a linear combination of all stocks which are allocated contributions according to their corresponding coefficients in the first principal component (that is, the combination explains the maximal variance in the data).
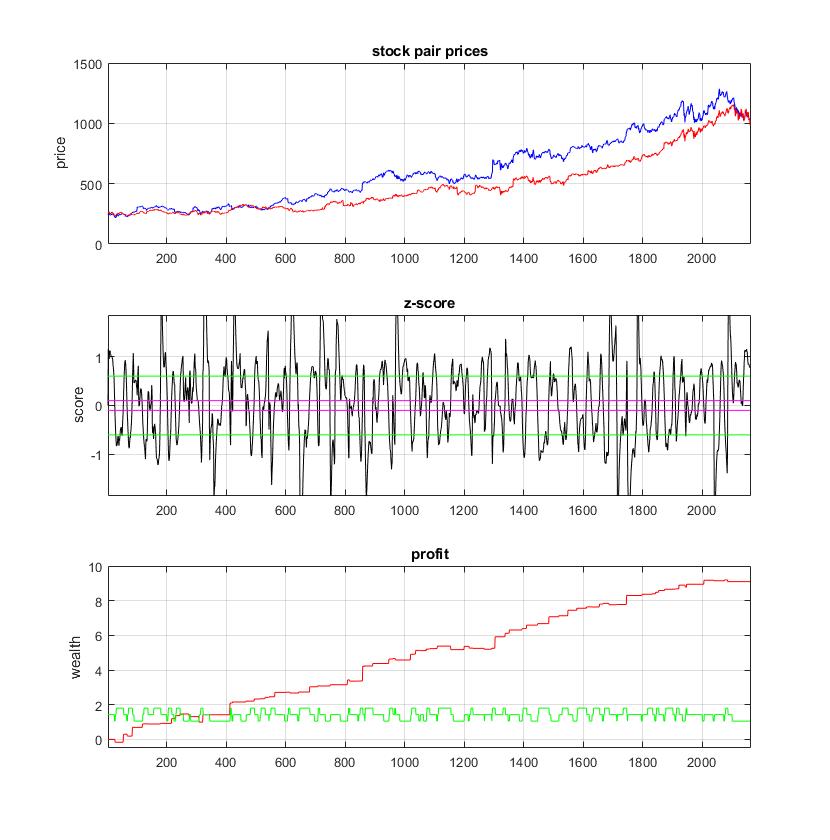
Machine Learning of Heavy-Tailed Dynamic Spread Models for Statistical Arbitrage. Statistical arbitrage is a trading strategy that analyzes the dynamics of mispricing in combinations of assets with the aim to exploit deviations from equilibrium levels in the markets, and generate buy/sell trading signals (so as to make profits before participants eliminate the arbitrage opportunities). The statarb technology identifies systematic market-dependent components from a slected set of assets, and computes the residual price difference (spread) from the remaining stocks in the portfolio. One popular idea is that the spread evolution follows a stochastic mean-reverting process. The mean reverting behaviour suggests that price divergencies will return back to their average, and this helps to take short/long positions as well as to build automated trading systems.
Our research develops machine learning tools for statistical arbitrage with continuous mixture models. These are continuous mixture models for mean-reverting spreads based on a discrete version of the Ornstein-Uhlenbeck stochastic differential equation. They are calibrated online with computationally efficient mixture filters to obtain plausible parameter estimates on the typically non-Gaussian financial data. Our tools have two distinctive advantages: 1) the filters are applied to heavy-tailed models elaborated with dynamic scale-mixtures of normal and gamma densities (that actually approximate Student-t distributions), and 2) they perform robust sequential Bayesian estimation of the parameters. Overall, these are learning machines that carry out predictive adaptation of the models to the changes in the markets via forecasting of their time-varying parameters.
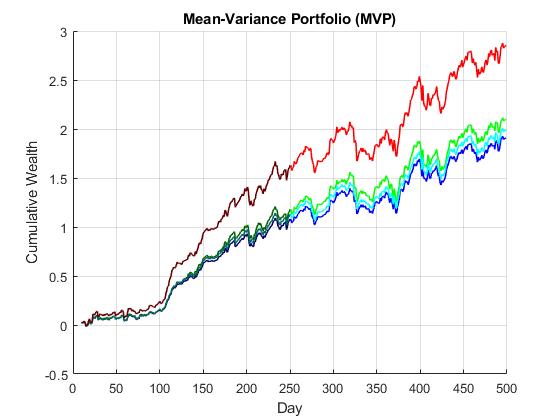
Deep Cleaning of Covariance Matrices for Portfolio Allocation. Covariance matrices are important in modern portfolio theory as they provide information about the collective movement of asset prices and help to achieve efficient portfolio selection. The covariance matrix shows the interactions between assets, and indicates which combinations can yield maximum profits with minimum volatility (reduced risk). The particular asset allocations (portfolio weights) are typically found by optimization using the sample covariance matrix. The estimation of the sample covariance matrix however is problematic: when there are many stock price series of limited duration their statistical characteristics can not be determined accurately as their computation accumulates significant errors. Robust portfoilios can be designed after cleaning the covariance matrix in advance.
Our research developed an original technique called Autoencoder Machine (AEM) for deep cleaning of covariance matrices. The AEM uses a deep neural network that learns parameters corresponding to the directions of maximum variance of the input data. The training searches for smoother network mappings and finds denoised versions of the eigenvectors of the covariance matrix which help to recover its genuine structure. The novel technique achieves such effects due to the following advantages: 1) it performs predictive cleaning in the sense that it enables to forecast the elements of the covariance matrix after training with the given past data; 2) it handles the given data with a heavy-tailed (Student-t) distribution which is well known to be more realistic for treating returns on prices; and 3) it uses a probabilistic Bayesian procedure for model calibration.
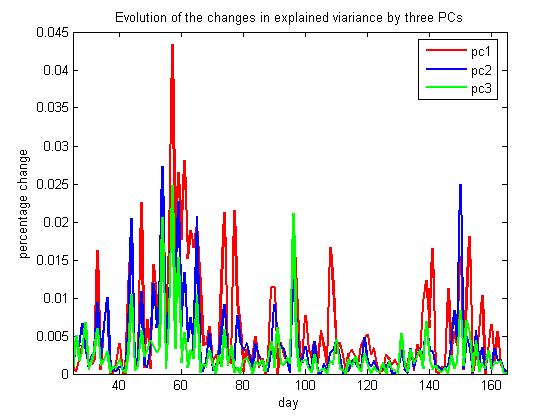
Forecasting Covariance Matrices via Deep Learning of Volatility Models. The task of portfolio construction involves search for asset allocations that can bring maximum profit with minimum risk. A key element in the mean-variance portfolio (MVP) framework is the covariance matrix (with second order moments) of returns. The challenge is to find faithful and useful estimates of the covariance matrix which lead to profitable portfolios on out-of-sample data. The covariances are often calculated by Exponentially Weighted Moving Averaging (EWMA) of historical returns. This sample-based approach however does not deliver good performance in practice. Recent research achieves improved results using approaches that forecast the covariances, like the Dynamic Conditional Correlation (DCC-GARCH), and the Generalized Principal Volatility Components (GPVC) analysis. Common in these approaches is that they build multivariate volatility models.
Our research developed a deep learning tool for multivariate nonlinear MNGARCH volatility models, which is suitable for construction of variance-based portfolios. This tool provides several original features: 1) it uses nonlinearities for enhancing the model potential to describe complex patterns in financial time series; 2) it treats the model with a proper temporal training algorithm which tracks the time-varying characteristics in the data and preserves the model dynamics; and 3) it uses the t-Student distribution in the training objective function for accurate fiting of data coming from heavy-tailed distributions (like returns on prices). The MNGARCH model is represented as a multi-output recurrent neural network. The network is trained with a temporal gradient descent algorithm (called Back Propagation Through Time (BPTT)) after unfolding it in time. This algorithm creates a deep neural network structure by making temporal copies of the nodes, and duplicating the memory as well as the recurrent connections. The operation of the learning procedure is robust thanks to the adoption of the heavy-tailed noise distribution, and it is not disturbed by occasional outliers in the data.
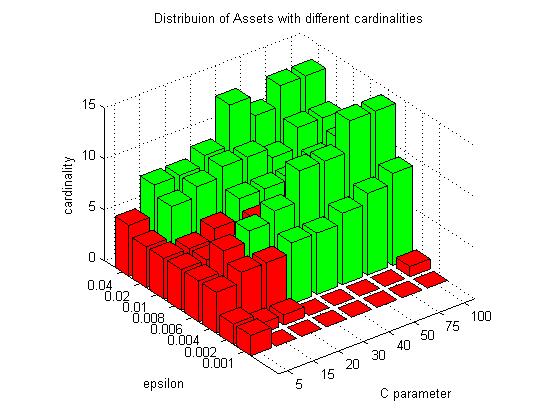
Support Vector Machine Learning of Sparse Portfolios. The portfolio construction task involves finding an optimal subset of assets for investment and estimating their allocations. An efficient method for solving both tasks simultaneously is to use high-dimensional regression models (where asset prices/returns are used as regressors and allocations as weights) with cardinality constraints. This is a numerically difficult problem because learning high-dimensional models from noisy, real-world financial data leads to weights that are not very precise. Overcoming such computational difficulties is important for the practical applicability of such models. The common strategy to mitigate these difficulties is to develop stable procedures that seek sparse models by shrinking the weights using regularization techniques.
Our research implemented a reformulated epsilon Support Vector Regression (e-SVR) machine for efficient and robust learning of portfolios (including the number of assets/cardinality and the weights/allocations). This reformulation enables fast and reliable convergence to unique globally minimal solutions (without using slow optimization procedures). The e-SVR minimizes the structural risk (which is a kind of generalization error consisting of fitting error plus regularization) and, that is why, it learns parsimonious models. The plausible values of the hyperparameters that govern the model complexity are found with a cross-validation technique using the available historical data. Actually there are two hyperparameters: the first determines the size of the sensitivity, and the second determines its influence on the magnitude of the fitting error.
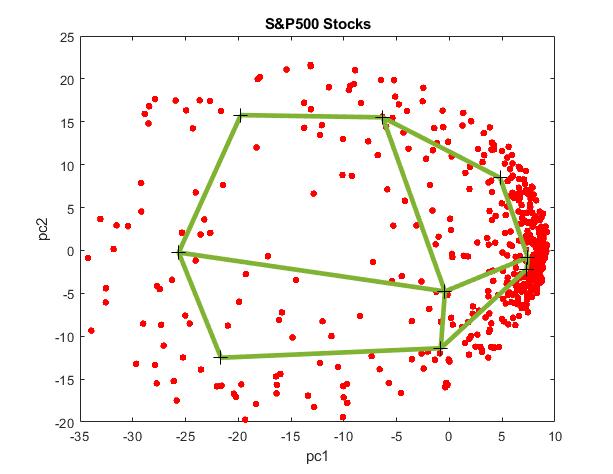
Finding Structure in the Co-movement of Stock Prices via Adaptive Metric Unsupervised Learning. Building portfolios involves stock selection by searching for relationships in the stock prices movements. Having determined the connections between the stocks one can partition them into clusters and apply various techniques for making portfolios. A clustering algorithm places time series into groups of similar elements with respect to a chosen distance measure. The group centers (centroids) are continuously updated to minimize the distance-based objective function so as to optimize the allocations. When handling time series of prices or returns the proximity measure should take into account also for the temporal variability in the sequentially arriving data.
Our research developed an innovative SOM network tool for clustering using a flexible transformation-based shape measure, which is especially appropriate for finding temporal patterns in real-world financial time series. This metric adapts the pattern from the chosen fair for comparison by linear transformation, which helps to update more precisely the cluster centroids. Stable performance is achieved using an incremental gradient descent training of the centroids. The architecture of the the self-organizing network is considered a two-dimensional rectangular lattice. The center weights are initialized with a random number generator.
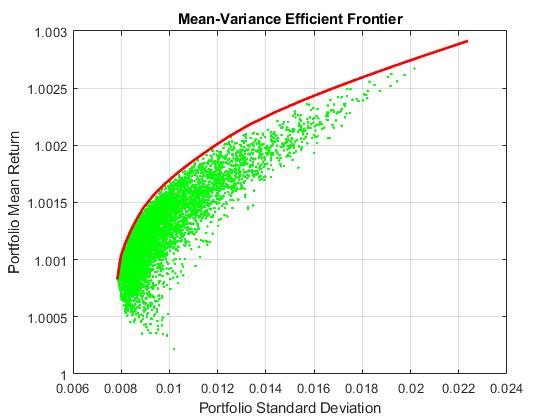
Robust Portfolio Optimization via Connectionist Machine Learning. The Mean-Variance Portfolio (MVP) of Markowitz is a popular model for investment diversification and management that helps to achieve maximized profits with reduced risk. It involves search for the amount of money to invest in each asset given the sample covariance matrix of asset returns, which is a constrained quadratic programming (QP) problem typically addressed using standard optimization routines. The QP in context of large scale financial applications is a difficult problem because the sample covariance matrix of stock returns is very noisy and this misleads the optimization procedures. The practical complication is that standard optimizers tend to overfit the noise while searching for solutions, and this leads to suboptimal results. One strategy for dealing with the noise is through statistical cleaning of the covariance matrix in advance.
Our research developed a QP optimizer with an embedded Multilayer Perceptron that elaborates on the good features of both: optimizers with stable convergence and neural networks with robust calibration. We implemented an original Connectionist Optimization Machine (COM) suitable for finding portfolio allocations. Its distinctive features are: 1) it conducts second-order search using the analytical derivatives of the neural network model,which leads to improved accuracy compared to the use of numerical derivatives (computed by differencing), and 2) it performs input denoising simultaneously with the learning of the model parameters, that is it removes the noise from the sample covariance matrix during calibration. It should be noted that adopting the framework of classical QP optimizers enables easy accommodation of various constraints in the training procedures.
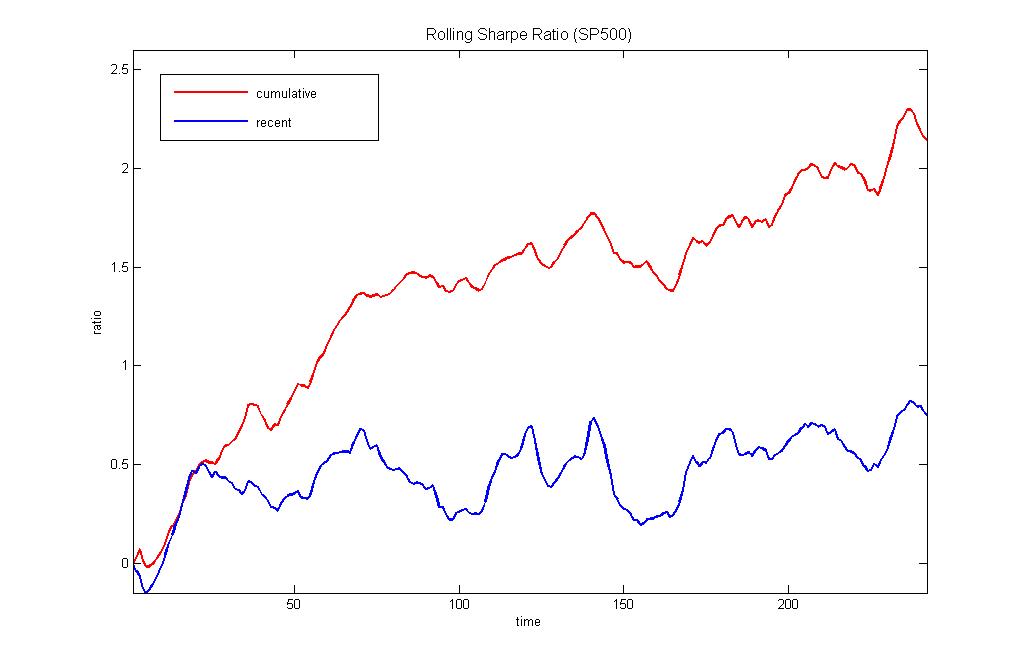
Online Portfolio Trading by Dynamic Reinforcement Learning. The computerized trading systems become increasingly popular due to the electronic nature of the transactions executed on most of the stock markets. Among the various computational algorithms for financial investing increasingly popular become the machine learning algorithms for building portfolios of assets. These learning machines offer potential for finding optimal allocations and suggest efficient rebalancing which helps to maximize profits while minimizing the risk. They carry out not simply statistical analyis of data, but also identify temporal dependencies that are useful for describing the evolution of sequentially arriving asset prices. Having such capacity is useful when searching for profitable allocations in a selected universe of stocks.
Our research developed a Reinforcement Learning machine for Online Portfolio trading (RLOP) using a recurrent neural network. The network model takes as inputs series of returns from the assets in the portfolio, and outputs allocations for each asset (the current version generates long only trading sugnals). The recurrent network is suitable for representing financial series as it is especially designed to learn from sequential data via an internal memory. The memory maintains short-term temporal information which influences subsequent outputs. This network is a dynamic model that we treat with a proper dynamic training algorithm, the so called BackPropagation Through time (BPTT). A distinguishing feature of our machine is that we implement the BPTT with a modern stochastic gradient descent technique for computing the temporal derivatives (it helps to obtain unbiased parameter estimates). This technique is further elaborated using adaptive learning rate for switching between passive and aggressive updating depending on the recent profitability.

Algorithmic Cryptocurrency Trading with Sharpe-optimal Deep Learning. Algorithmic trading uses computer programs to analyze market data and generate trading signals with suitable models. Particularly appropriate for such tasks are the neural networks due to their ability to learn flexible nonlinear models with good predictive capacity. The problem is how exactly to train these networks on financial price data so as to produce useful trading decisions, because prices are very difficult (practically impossible) to forecast. Since prices are considered to follow Geometric Brownian Motion, it can not be expected the neural network learning machinery will induce sufficient predictive potential simply by fitting the data with error-minimization procedures. Better results can be obtained by training the neural network parameters on price returns using directly a financial objective instead of a fitting criterion. Thus, the model can be adapted just to capture the directional fluctuations in the given series which are sufficient for sending trading signals. The financial objective to achieve high profits with low risk can be specified with different formulae, like the Sharpe ratio for example.
Our research developed a Sharpe-optimal Deep Learning (SDL) machine suitable for high-frequency algorithmic trading. A feedforward deep neural network is elaborated to predict the position size (which serve as a corresponding buy/sell trading signal) given a time series of relative price returns. The deep neural network brings increased flexibility for enhanced nonlinear modeling through a tuneable multilayer structure, including rectified units (leading to sparsity) and sigmoidal units (providing nonlinearity). The network model is trained with a risk-adjusting backpropagation algorithm that implements gradient ascent in the performance space. The performance is measured with a modified Sharpe ratio that discounts effects from the loosing trades. This helps to overcome equal treatment of high profits with heavy loses in the alternative standard deviation formula. During training the neural network continuously improves its skills to take useful trading decsisions (without external supervised help).
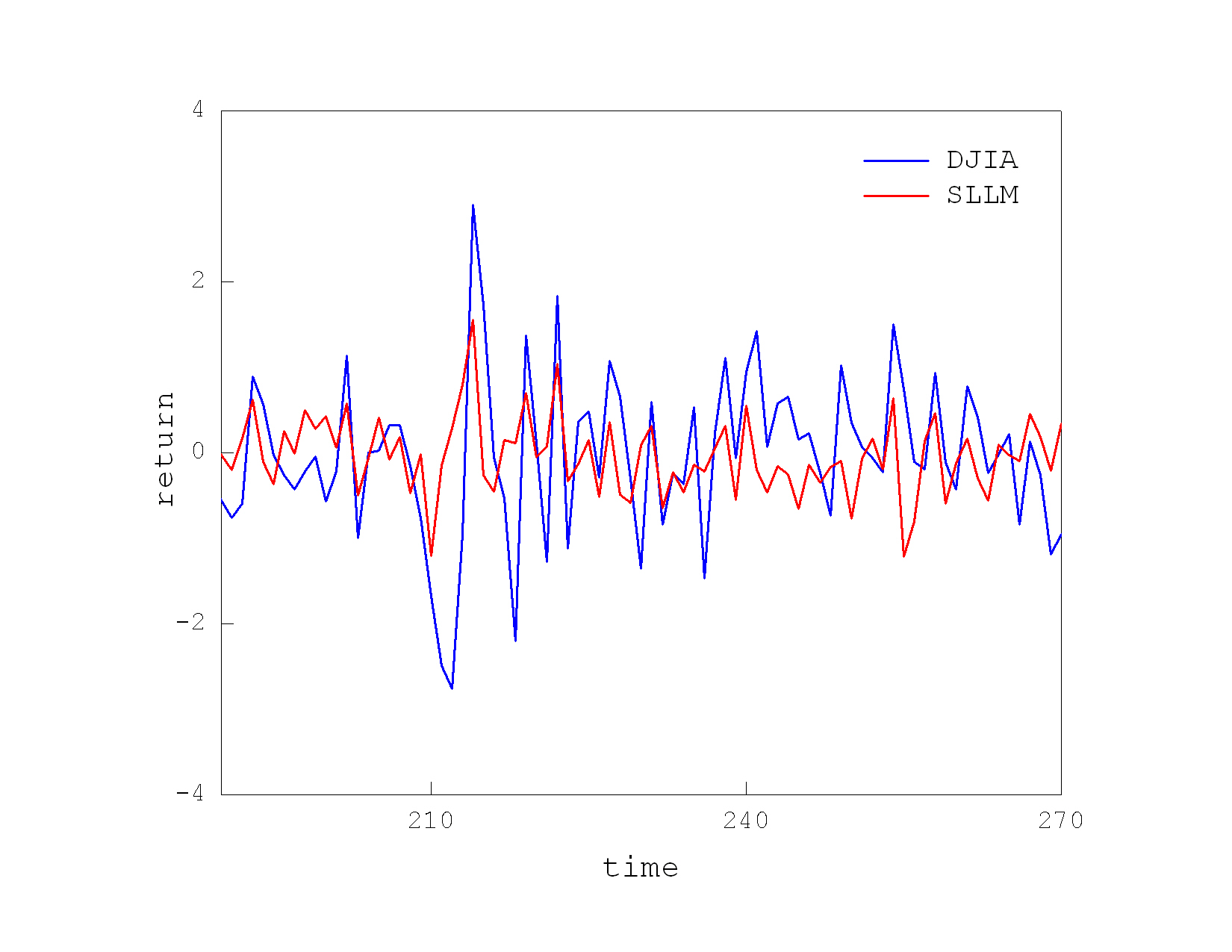
Self-Tuning Local Learning Machines for Prediction of Stock Market Returns. Current advances in machine learning provide various sophisticated models for predicting financial time series. The selection of a proper learning strategy is extremely important for the success of the time series modelling technology. Processing directly price series (after detrending) requires global methods of high dimensionality because such series typically feature long distance autocorrelations. For example, one can develop deep-memory models using internal or external memory. Processing returns on prices requires local models of low dimensionality as return series typically show low autocorrelations. The nearest neighbour approach to local learning is especially appropriate for describing stock return movements because it is less affected by the changing autocorrelations in price series depending on the volatility.
Our research invented a Self-tuning Local Learning Machine (SLLM) that performs nearest neighbour regression especially for predicting financial time series. It performs self-adaptive translations of the neighbouring vectors during both phases selection and forecasting. The SLLM is original and involves two elaborated phases: 1) Invariant neighbour selection- it takes a predefined number of nearest patterns using an invariant distance metric to determine the proximity after linear transformations of the vectors, the metric accounts for the changes in the magnitude and period for accurate estimation of the nearness; 2) Local movement extrapolation- the prediction is made by averaging over the future series movements after the neighbours. The predicted next series values accommodate effects from the adjusted shapes formed by the changes in the series amplitude and trend. This is a kind of iterative extrapolation, rather than forecasting with coefficients obtained by fitting.
Deep Learning of Heteroskedastic Volatility Models for Risk Estimation. The volatility (changing variance) in time series of returns on assets impacts the pricing of financial instruments, and it is a key concept in automated algorithmic trading, option pricing, portfolio management and financial market regulation. The common assumption is that the return volatility is highly predictable. Popular tools for capturing the variance of the return distribution are the Generalized Autoregressive Conditional Heteroscedastic (GARCH) models. These models however are difficult to estimate (typically by maximum likelihood optimization) and suffer from mistakes, which limits their practical usefulness.
Our research developed a deep learning algorithm for dynamic heteroskedastic volatility models (D2GARCH) made as recurrent neural networks. The learning algorithm for D2GARCH creates a deep connectionist structure by unrolling the network in time. The unravelling is a process of transforming the temporal correlations into spatial relationships. The temporally dependent nodes and the recurrent connections are duplicated at each time instant, which leads to a deep topology of unfolded layers with shifted in time inputs trainable with static gradient-based algorithms. Then, the error is backpropagated through time (BPTT) in the sense that it is passed backward through the unrolled in time network, and the model parameters are adapted gradually to reflect the time ordering in the data sequence. Since the temporal error gradient decays and may vanish due to the unfolding (so it fails to contribute to the learning process), we apply the Kalman filtering technique to diminish such effects and to speed up the convergence.
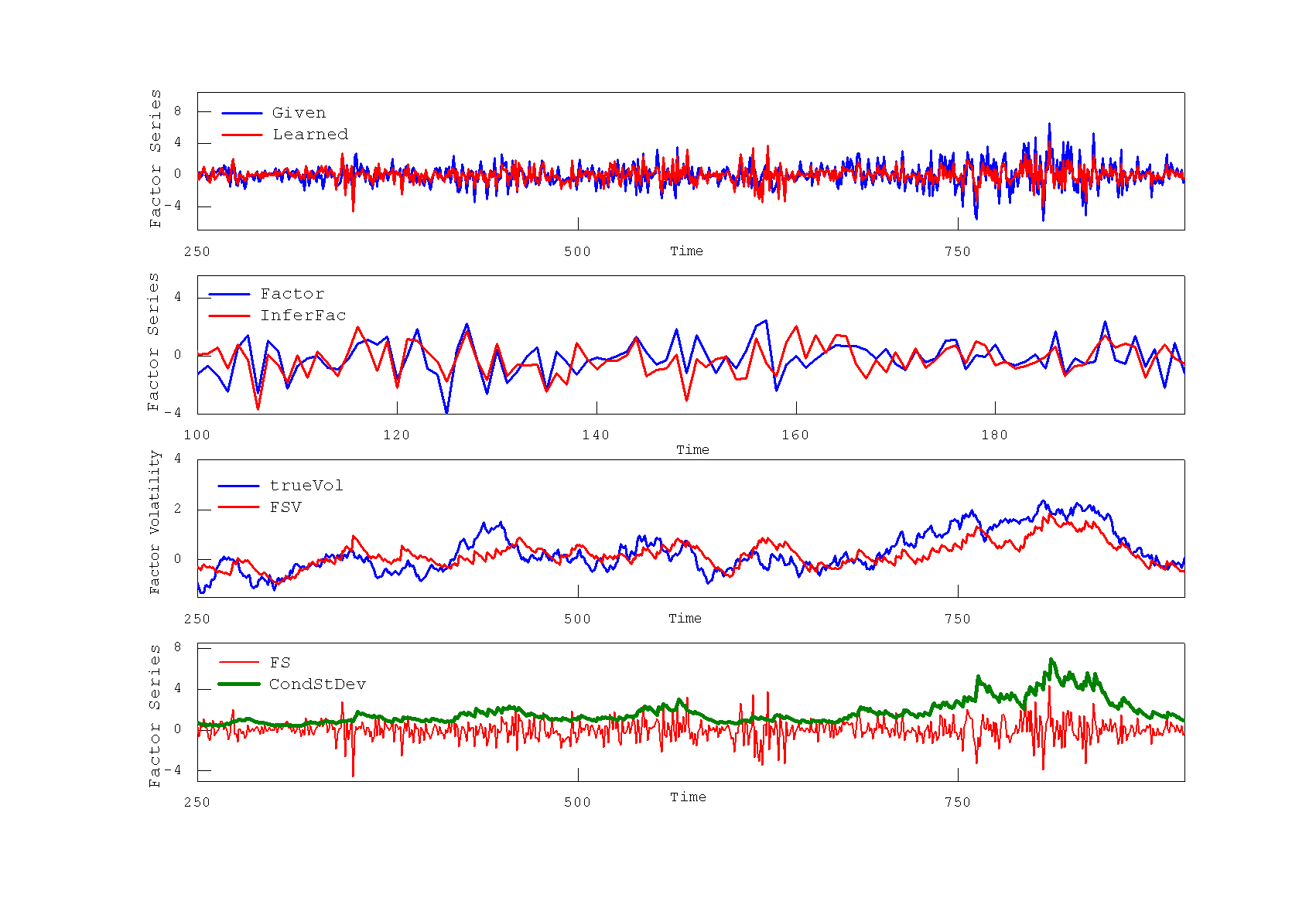
Analytical Factor Stochastic Volatility Modeling for Portfolio Allocation. Factor Stochastic Volatility models exploit the predictability of time-varying returns and facilitate optimal portfolio allocation. The stochastic volatility models are attractive for describing changing variances in fiancial data because they allow perturbations by random shocks in the model, which are independent from past information unlike the well known GARCH models. The problem of evaluating their likelihood and finding exact solutions has been addressed with various techniques, the most typical from which are Monte Carlo (MCMC) sampling and quasimaximum likelihood (QML).
Our research developed an analytical factor stochastic volatility (AFSV) approach to model estimation with closed-form expressions without using expensive sampling. Adopting the FSV model of Pitt and Shephard we show that all parameters, including the factor loading matrix, the noises and persistancies of the factor as well as idiosynchratic series, can be obtained with formulae derived to maximize the complete likelihood. We implemented a Nonlinear Quadrature Filter and a Smoother (NQFS) which treat the SV directly as a nonlinear model. The NQFS approximates the volatility distributions via recursive numerical convolution using the Gaussian quadrature scheme. Our NQFS makes Gaussian approximations to the (prior and posterior) distributions of the volatility, but not in the observations space. This one-step measurement updating helps to infer distributions with more complex shapes,and this is an improvement over most other numerical integration filters. After filtering and smoothing, the complete log-likelihood of all data is obtained in closed-form and the parameters (state noise, observation noise, and persistance) are estimated according to the Expectation Maximisation (EM) algorithm.
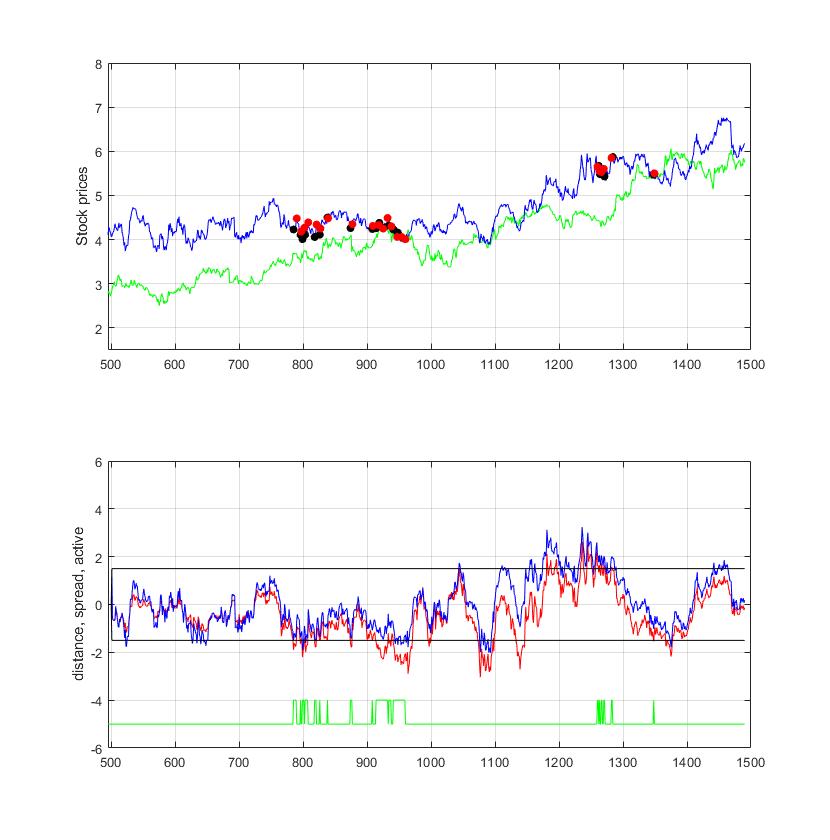
Pairs Trading with Markov Regime-Switching Filters. Pairs trading is a kind of statistical arbitrage which composes simple low-risk portfolios from two assets whose price movements are found correlated. Having a pair of assets the idea is to take a short position on the overvalued asset, and a long position on the undervalued asset. If the the evolution of the price difference (spread) between the assets is captured well one can accumulate profit in the short term. The differences in prices are taken to trigger trading decisions made with specific strategies, and the portfolio is rebalanced periodically depending on the reversion rate. The common assumption is that the spread from the cointegrated assets follows a mean-reverting process.
Our research developed a computational tool for modeling price differences based on a discrete version of the Ornstein-Uhlenbeck stochastic differential equation. The adopted mean-reverting spread model is calibrated with a Markov regime-switching filter to obtain plausible parameter estimates on the typically non-Gaussian (heavy-tailed) financial data. Such switching models emit mixtures of Gaussians governed by unobservable regime variables, thus providing potential to fit flexibly data distributions with non-Gaussian shapes, as well as to describe more accurately non-stationary financial time series. The spread is represented via regimes of high and low means, and this helps to predict when it reaches extremal points before returning back to equilibrium. After that, regime dependent arbitrage rules are applied to make profitable risk-neutral market strategies.
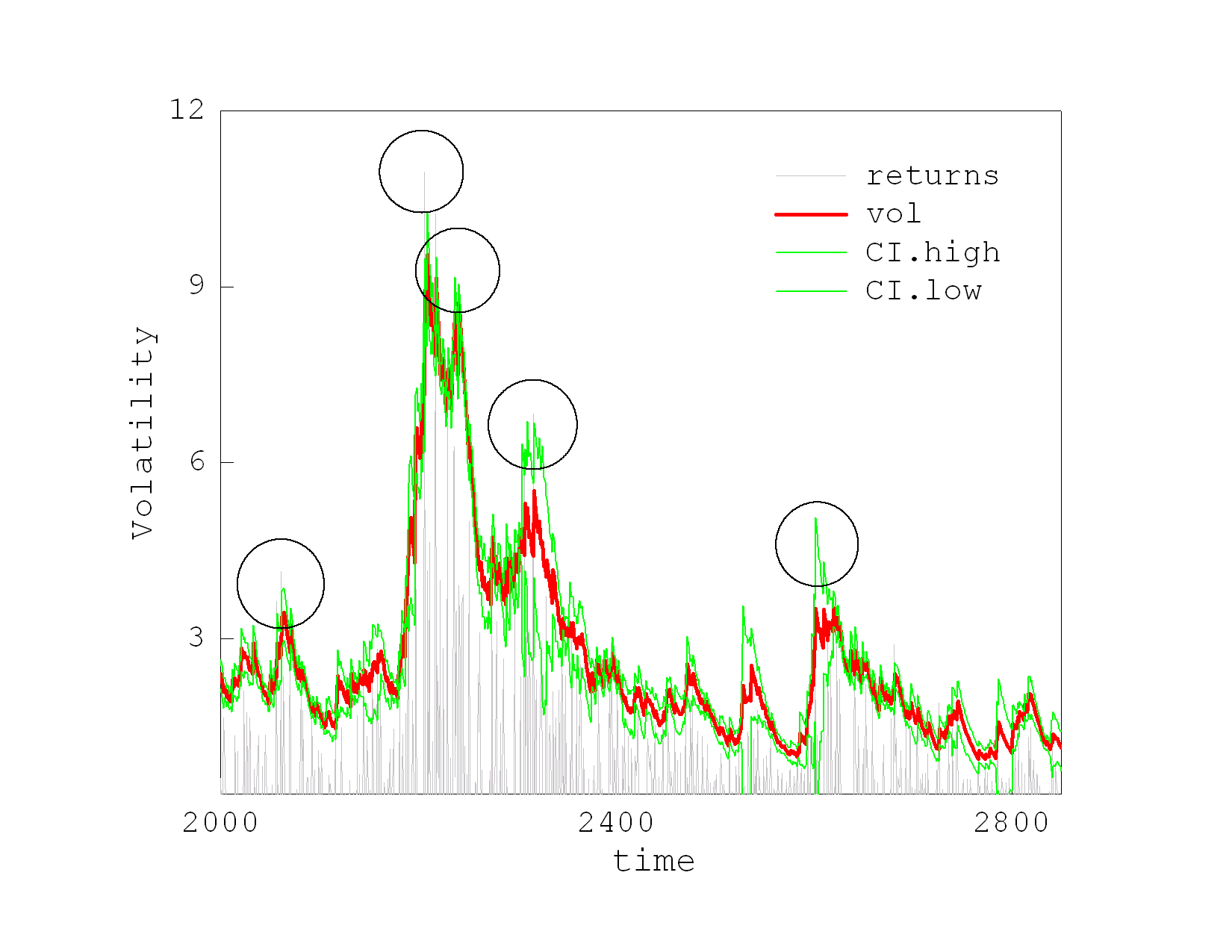
Value-at-Risk Estimation using Asymmetric Stochastic Volatility Models. The Value-at-Risk (VaR) is a risk measure which tells us the maximum loss that may happen with a certain confidence over a given time period because of the market prices fluctuations. The VaR is associated with the time-varying quantiles of the return distribution, and the VaR can be evaluated by simulating the predictive distribution of returns using bootstrapping. This technology involves computing one-step-ahead volatility forecasts, and rolling sequentially by one-step foreword over the testing subseries.
Our research developed a nonlinear filter for asymmetric stochastic volatility models that facilitates accurate empirical VaR stimation and compensates for the uncertainty in the model parameters. The nonlinear filter evaluates the moments of the prior and posterior volatility densities via recursive numerical convolution, and thus it obtains more efficiently the likelihood than the sampling algorithms. Both volatility densities are treated by Gaussian approximations using quadratures. A distinguishing feature of this Nonlinear Quadrature Filter is that it relies on the Gaussian assumption for both prior and posterior volatility densities, but not for the observations space. This is a key advantage over most other numerical integration filters and allows us to handle distributions with more complex shapes. In order to deal flexibly with financial series we design a version NQFSt that handles heavy-tailed data using the Student-t distribution.
Volatility Forecasting with Bayesian Kernel Models for Trading Straddles. Buying and selling straddles (combinations of call and put options with the same starike price and time to maturity) is often performed using volatility trading strategies that do not rely on option price changes. They assume that the straddle prices are sensitive to their volatility, and suggest to buy (sell) straddles when their predicted volatility increases (decreases). Straddles are typically traded using direction forecasts of daily (implied) volatility differences in the underlying indexes. This technology involves calibrating volatility models with pre-computed implied volatilities according to the inverted Black-Scholes formula using historical option prices.
Our research developed a Bayesian volatility forecasting framework using kernel models for trading straddles. These are probalilistic kernel machines trained with automatic relevance determination to carry out automatic model selection. The training is accomplished by iterative maximization of the marginal likelihood of the hyperparameters following the evidence procedure (using a specific noninformative prior over the weight parameters to obtain more stable hyperparameters). During the learning process some hyperparameters grow thus causing their corresponding weights to shrink toward zero. Our Kernel Machines showed superior trading performance compared to other popular machine learning models, like feedforward Neural Networks and Hidden Markov Models, on real-world series of daily closing values of the German stock index DAX together with a series of daily losing prices of call and put options on the DAX with different maturities and exercise prices.
Modelling the Stochastic Volatility of Exchange Rates with Monte Carlo Filters. Accurate pricing of financial instruments and sucessfull trading can be achieved using estimates of the volatility. There are various approaches to finding the volatility (considered as an an unobsrved component in financial time series) of price series, like the classical GARCH models and the stochastic volatility (SV) models. The SV models are found empirically more successfull than GARCH models as they capture better second-order properties of the returns as well as leverage effects. Popular techniques for SV inference are the particle filters. They use Monte Carlo samples, called particles, whose averaging allows to compute very accurately the characteristics of the posterior distribution of the unknown parameters.
Our research developed efficient Gaussian Sum Particle Filters (GSPF) for learning stochastic volatility models from series of returns on prices. These GSPF use Gaussian mixtures to represent all the distributions of interest, including the noise on the latent parameters. Representing even the noise on the unobserved parameters by a mixture density increases the descriptive potential of the filter, and makes it more flexible when processing oscillating series. An important advantage of GSPF is that they attain good results with acceptable computational speed, due to the need to maintain a small number of particles than previous filters. The experimental investigations demonstrate that GSPF achieves better statistical characteristics (smallest deviation from normality, lower autocorrelations, and higher likelihood) than the benchmark GARCH, as well as Particle and Auxiliary Particle filters when applied to infer the volatility of GBP/USD exchange rates series.